POSTS

• 2026-01-10 Structure your experiment's results using hive partitioning

  If you structure your experiment's results in a certain way, you get the loading almost for free using duckdb.

• 2025-02-16 The future of black box optimization benchmarking is procedural

  Recent work by Saxon et al. highlights the need for dynamic benchmarks, and I think procedural content generators might provide an answer.

• 2024-06-21 Mapping high-dimensional Bayesian optimization using small molecules

  Starting a map of high-dimensional Bayesian optimization (of discrete sequences) using small molecules as a guiding example

• 2024-03-16 Do Gaussian Processes scale well with dimension?

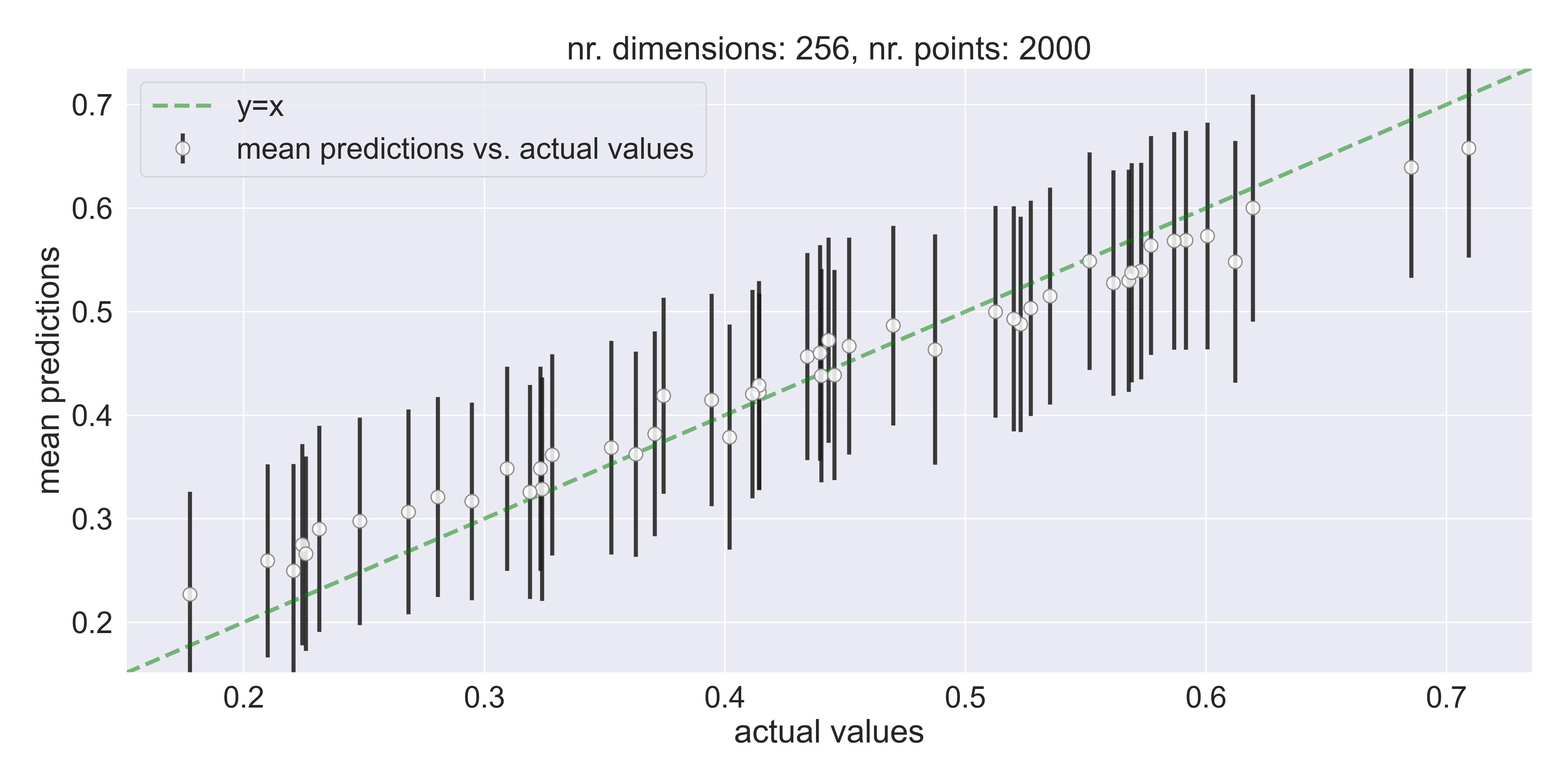
  This blogpost implements a small experiment to check when and how Gaussian Processes fail in high dimensions, and explains recent research on the subject.

• 2023-07-31 Bayesian Optimization using Gaussian Processes: an introduction

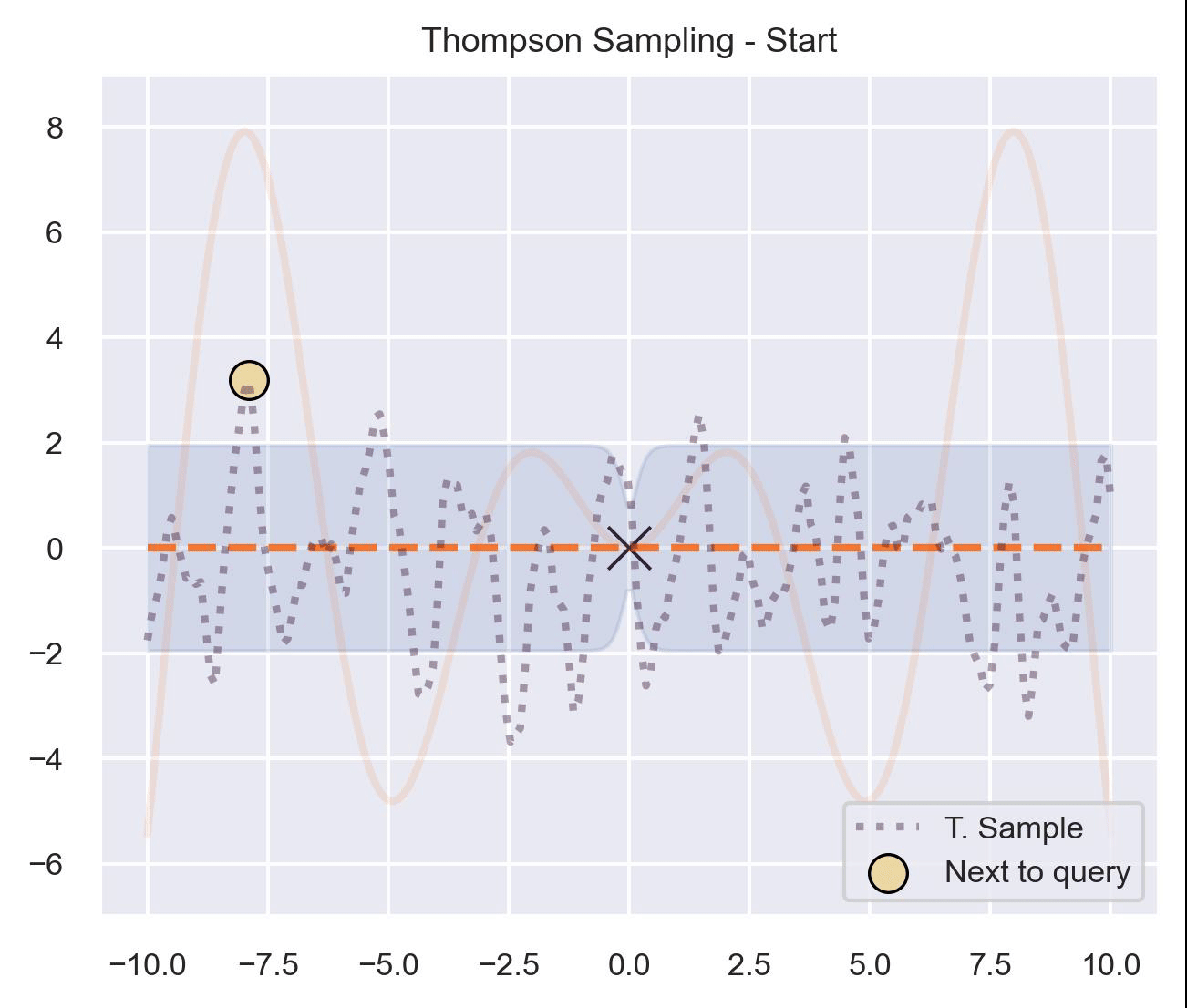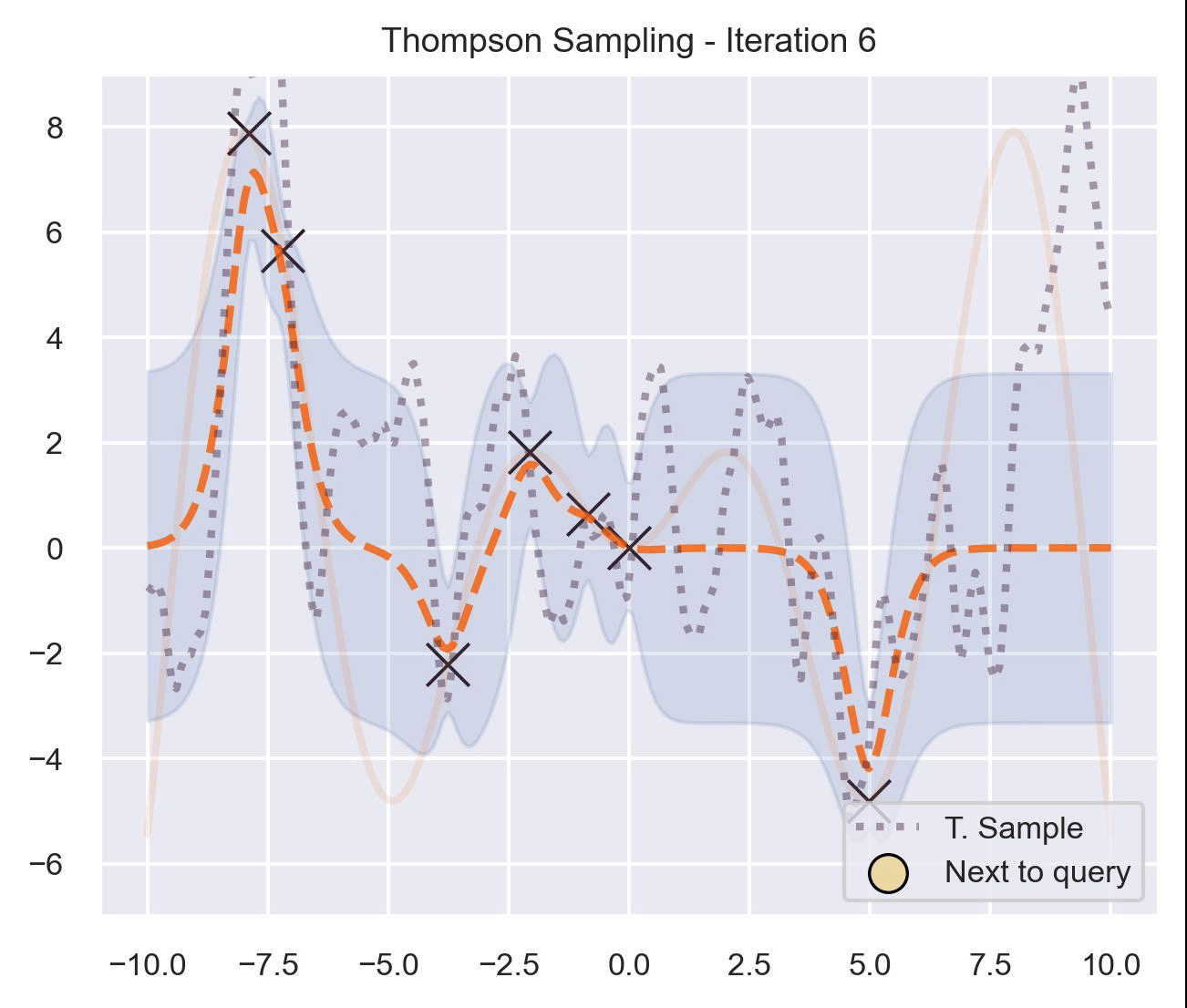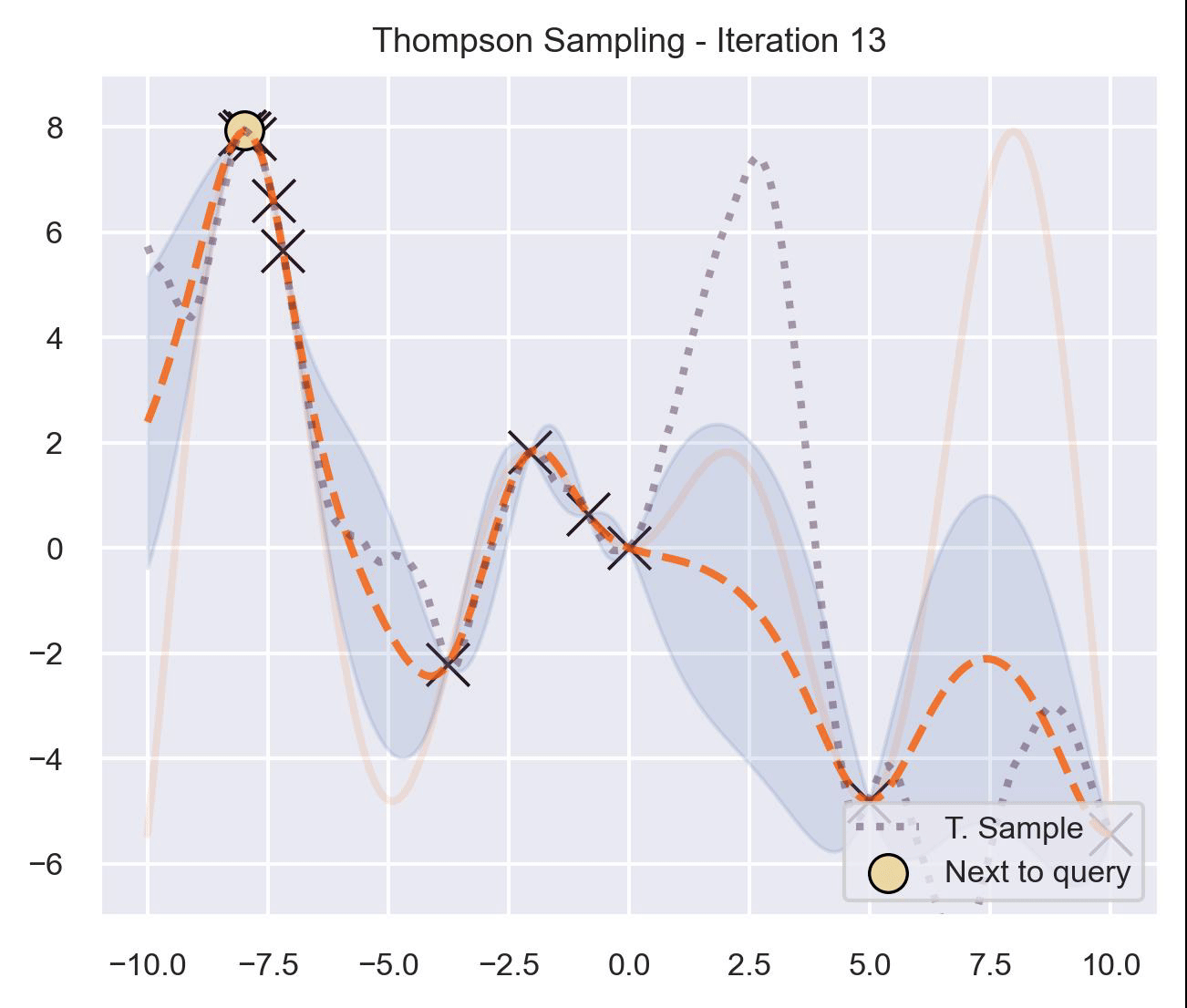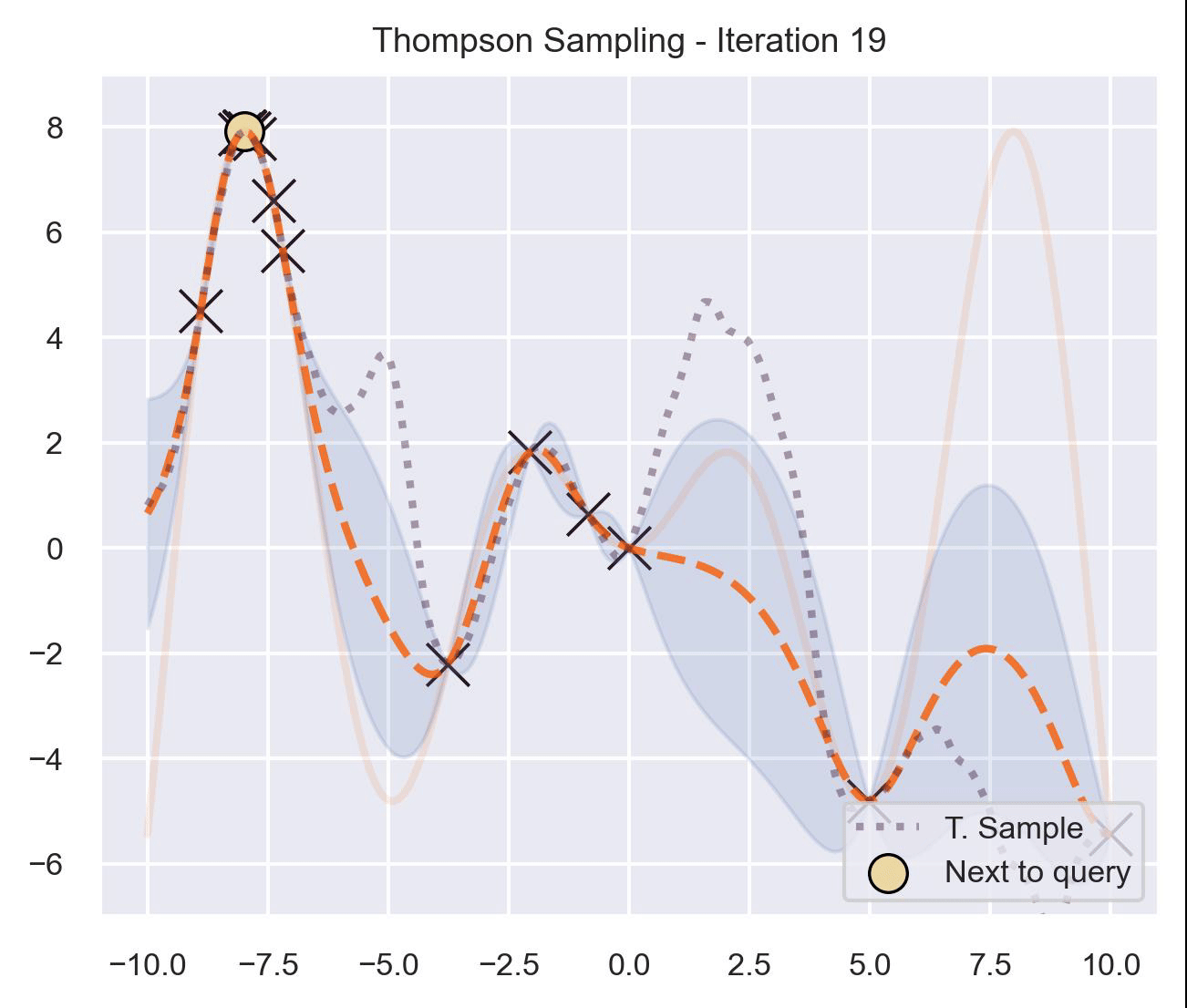
  An introduction to Bayesian optimization using Gaussian Processes.

• 2022-05-23 Training a VAE on Super Mario Bros and playing its levels

  Representing levels from Super Mario Bros as strings, and learning a continuous representation using Variational Autoencoders.

• 2020-12-24 On Stuttering

  An essay on stuttering, my experience, and a little bit about the neuroscience behind it.

• 2020-12-15 Translating measure theory into probability

  a Rosetta stone, showing how basic concepts in measure theory (e.g. a measurable functions) correspond to concepts in probability theory (e.g. random variables).

• 2020-01-15 Creating Priors using Normal Noise

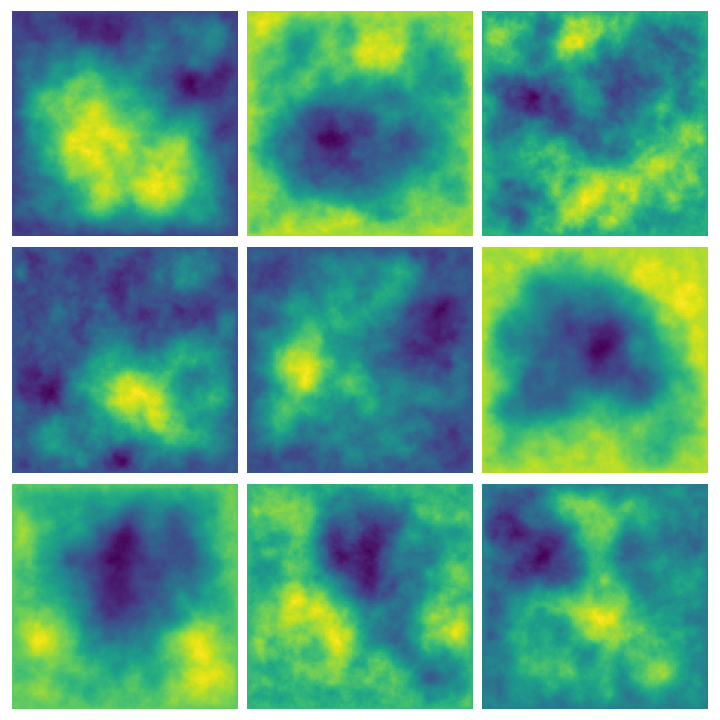
  In this blogpost I share a technique to generate random priors from Gaussian noise (by having the noise model the slope/curvature of the prior).

• 2019-10-25 Creating a random graph from a string

  Generating random graphs using strings to seed the number generators.

• 2019-10-06 A Link to my MSc Thesis

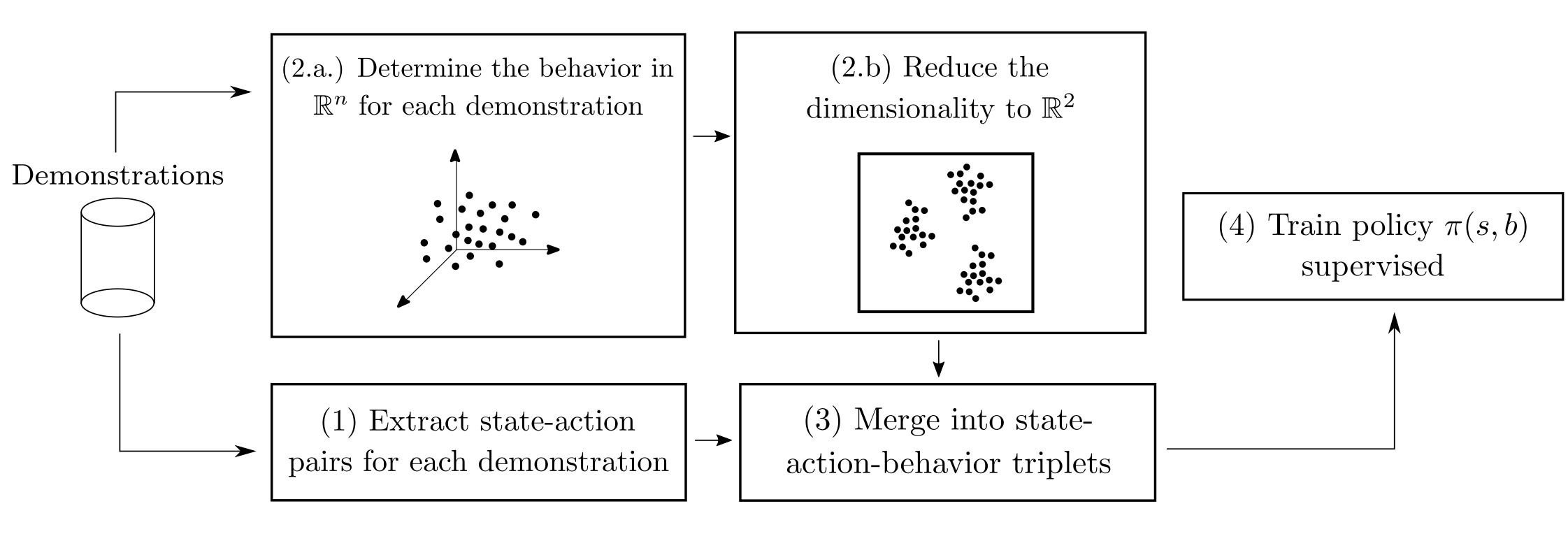
  I recently defended my MSc thesis on applications of imitation learning to StarCraft 2. Here is a link to it.

• 2018-09-03 A tutorial on sc2reader: events and units

  The package `sc2reader` is useful for extracting data from replays of StarCraft 2. This blogpost provides a small tutorial on how to use it.

• 2018-01-24 Latin Squares and Finite Groups

  A proof that there are only two groups of order 6, using only combinatorial arguments.

• 2018-01-18 A couple of metrics in generalrepytivity

  A small tutorial on `generalrepytivity`, a Python package to manipulate tensors in differential geometry.